Hexagonal Tangram Filling

The goal is to develop an algorithm that counts all possible solutions for filling the hexagonal Tangram using its 11 original pieces. To achieve this, the idea is to decompose the Tangram into equilateral triangles, noting that each piece consists of either 3 triangles (the 4 trapezoidal pieces) or 6 triangles (the other 7 pieces). The four trapezoidal pieces can be grouped into two larger pieces of 6 triangles, creating an alternative version of the problem with only 9 pieces, which reduces the number of possible solutions, making the problem more challenging. The algorithm also accounts for this variation (polymorphism).

Enumeration of Tangram Solutions

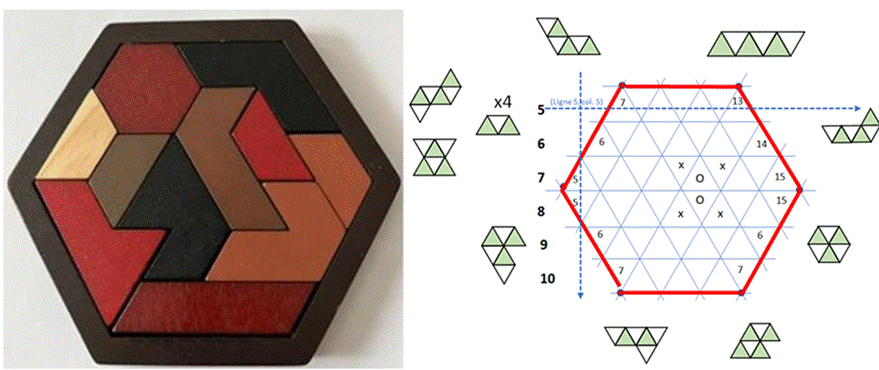
There are several types of pieces, each characterized in the algorithm by the number of ways they can be placed on the Tangram. These placements are called variants. To simplify the identification of pieces, each one is given a name. The initials of these names, in French, are used to describe the solutions.

Summits and piques refer to the orientation of the triangles in the hexagonal grid. Summit refers to a triangle with its apex pointing upward and Pique refers to a triangle with its apex pointing downward.

The algorithm systematically scans all triangles of the Tangram in a predefined order, starting from the top left. When a piece is placed, it searches for the next available triangle and attempts to place another piece. The Tangram's triangles alternate between pointing upward (summit) and downward (pike). Given this traversal order, the chosen triangles for placing a piece is always the uppermost and leftmost triangle of the selected variant, as all triangles above or to the left of an already placed piece are occupied. The algorithm iterates over all permutations of the pieces, as well as over all pieces and their variants. The main loop (permutation of pieces) is independent of the Tangram: since there are 11 pieces, including 4 identical ones, the number of unique permutations is 11! / 4! = 1,663,200.

A secondary loop, nested within the main loop, attempts to place each piece and its variants in the order determined by the main loop. This secondary loop, which depends on the shape of the Tangram and the pieces, is the core of the algorithm. Once all possible combinations have been exhausted—whether solutions have been found or not—the secondary loop hands control back to the main loop, which then processes another permutation of the pieces. When a raw solution is found, it can logically generate 11 additional solutions through geometric transformations. Each solution belongs to a family of 12 solutions, which are equivalent under symmetry and rotation transformations. Within this group, the first raw solution found by the algorithm serves as the reference solution. The coordinates of each piece are defined relative to a reference point (0,0), which corresponds to the triangle where the piece is placed on the Tangram. When a piece is positioned, all its triangles are translated according to its placement within the Tangram's coordinate system. A solution is characterized by the list of 11 placed pieces, each with its specific placement variant. For example, it can be represented by the sequence: "Bs0Cs0Fs0Tp0Tp1Ps3Hs0Ts0Ls4Sp1Ts0"

This ASCII string uniquely identifies the solution.

Each placed piece is defined by a name, an initial letter representing that name, and its variant. The name initials are uppercase letters. In the example above: B, C, F, T, T, P, H, T, L, S, T.

The two characters following each piece's initial represent its variant, identified by a letter and a number:

Ø "p" indicates that the piece is placed on a downward-pointing triangle (pike).

Ø "s" indicates that the piece is placed on an upward-pointing triangle (summit).

Ø The number corresponds to the specific variant of the piece within that triangle type.

Having the variant information is essential to reconstruct the solution: it serves as the Rosetta Stone of the Tangram.

There are 42,348 raw solutions for the Tangram with 11 pieces and 108 raw solutions for the version with 9 pieces. As expected, the number of raw solutions found is a multiple of 12, resulting in only 3,529 reference solutions. Among these 3,529 reference solutions, 62 divide the Tangram along a straight line, while 114 position the hexagon at the center of the Tangram.

Grouping Solutions into Families

It is reassuring to find that, in both cases (11 or 9 pieces), the number of solutions is a multiple of 12. However, the algorithm does not establish any relationships between solutions; it simply identifies solutions without correlating them. The second phase consists of verifying that all these solutions can be grouped into families of 12 elements.

A more complex algorithm than the solution-finding algorithm was developed for this purpose. It uses the results from the counting algorithm and in the case of the 11-piece Tangram, the list of 42,348 raw solutions. Each solution found should theoretically generate other solutions forming an equivalence class of 12 elements, linked by geometric transformations, including rotations (60°, 120°, 180°, 240°, 300°), optionally combined with axial symmetry through the Tangram’s center. If the algorithm is correct, these transformed solutions should already exist in the list of raw solutions.

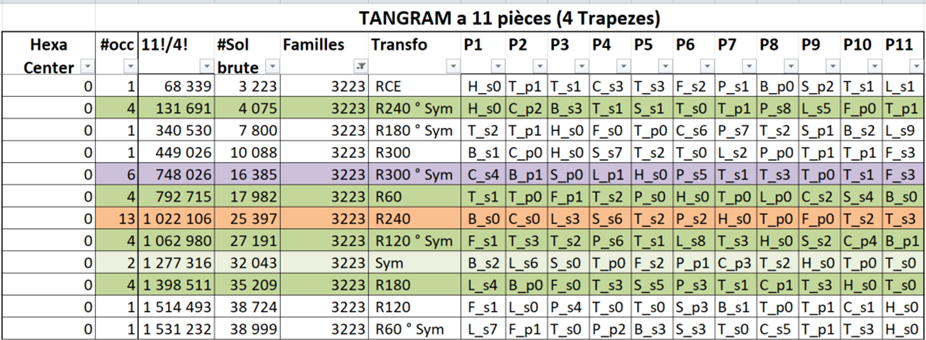
This second algorithm performs that task, grouping the 42,348 solutions of the 11-piece Tangram into 3,529 families (exactly 12 times fewer). For the 9-piece Tangram, there are 108 solutions forming only 9 families. The absence of isolated solutions further supports the completeness of the solution set. An example of an equivalence class is shown below. The Representative of the Equivalence Class (RCE) is the index of the first raw solution found. The equivalence class algorithm then searches among all known solutions for those associated with each RCE. An example of a family and its transformation relationships is presented below. The family number (12,334) corresponds to its RCE. The 11 other solutions in the same family (12,334) are derived from simple geometric transformations of the RCE solution.

Notably, the 12 indicated transformations (11 transformations plus the identity, which leaves each piece unchanged) form a mathematical group under composition.

The complete set of results, including solutions and their grouping into families, is documented in the accompanying Excel file. The "Transfo" column specifies either the Representative of the Equivalence Class (RCE) for the first solution found or the geometric transformation (e.g., R240° Sym) required to obtain another solution within the same class. For instance, R240° Sym represents a transformation composed of a horizontal symmetry followed by a 240° counterclockwise rotation. The "Sol 9_11" sheet lists all solutions for both the 9-piece and 11-piece Tangram problems, while the "correlation9" and "correlation11" sheets organize the equivalence classes and the 12 solutions associated with each class.

Visualization of the solutions

Each string identifies a solution, but does not present it: it's the reader's job, with the help of the "tangram Rosetta stone", to place the pieces. The following link presents a solution visualization tool for 11-piece tangrams. The 9-piece tangrams are displayed below.

Relations between Solutions

Since 42,348 solutions are found, the algorithm identifies approximately one solution every 40 orders (meaning one solution for every 40 permutations of the 11-piece Tangram).It is observed that certain piece orders allow for multiple solutions. The table shown indicates that 16,236 orders result in multiple solutions, ranging from 2 to 13 solutions per order.

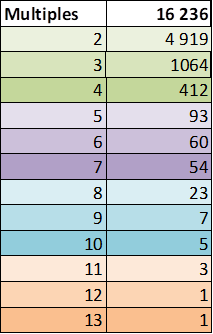
As expected, the trapezoidal piece provides greater placement flexibility compared to the other pieces, making it easier to obtain distinct solutions within the same order.

This multiplicity property is illustrated with an example where three distinct solutions (raw solutions 39,735, 39,736, and 39,737) originate from RCE families 1172, 1174, and 1173 through a 120° transformation. The order number (permutation of the pieces) selected for this example is 1,560,069. The #occ value indicates the number of multiple solutions found for this order.

The geometric transformations of multiple solutions do not preserve the initial piece order in the same way for all multiples. A multiple solution found from a specific piece order does not necessarily imply that all other solutions in the same family will also exhibit multiplicity. This can be explained by the fact that the order of placement follows a very specific rule, which prioritizes positioning pieces toward the top-left. The example above provides a clear illustration of this property.

The raw solution 33,274, found using order 1,351,206, belongs to family 1174 but does not have multiple solutions. In contrast, solutions 38,002 and 38,003, derived from the same piece order (1,502,466), exhibit multiplicity of order 4, differing from the previous case, which had order 3. The table below identifies the piece permutation number 1,022,106, which produces the highest number of raw solutions. These solutions, generated under the same permutation, have a multiplicity of 13.

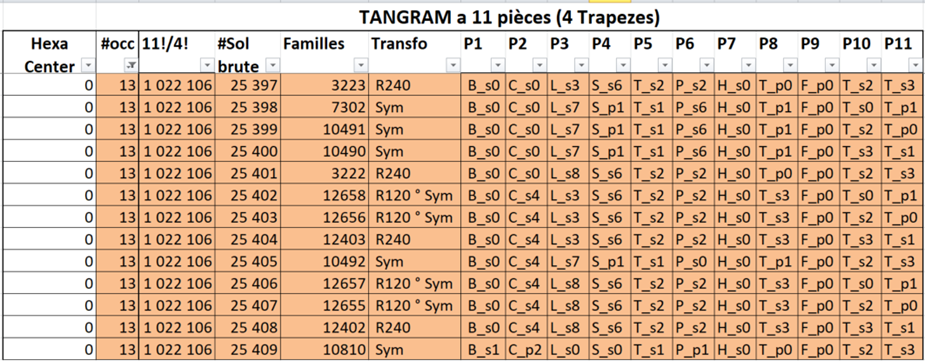
The first raw solution (25,397) belongs to family 3,223. The multiplicities of the different members of this family range from 1 to 13, as shown in the table below.

Representatives of the solution families for the 9-piece Tangram